How Lucky Are You?
I’ve been thinking a lot about numbers recently. I have a degree in Electrical Engineering so a lot of my life has been wading hip deep in numbers, statistics, and complex math. As a fellow who likes games and seeks to play them well, I often find myself turning to data analytics to understand what trends are successful and what strategies are faring poorly. Data can come from lots of places. Online games often have huge communities dedicated to analyzing and crunching the results of competitions. Heroes of the Storm has hotslogs.com. Guild Wars 2 has Metabattle.com. Magic the Gathering has mtgdecks.net. Back in the day World of Warcraft had Elitist Jerks and their affiliated websites. Basically any popular game you can think of has a wiki curated by the community, constantly throwing shit at the wall to see what sticks. In the course of this analysis, some strategies rise to the top while others fall out of favor.
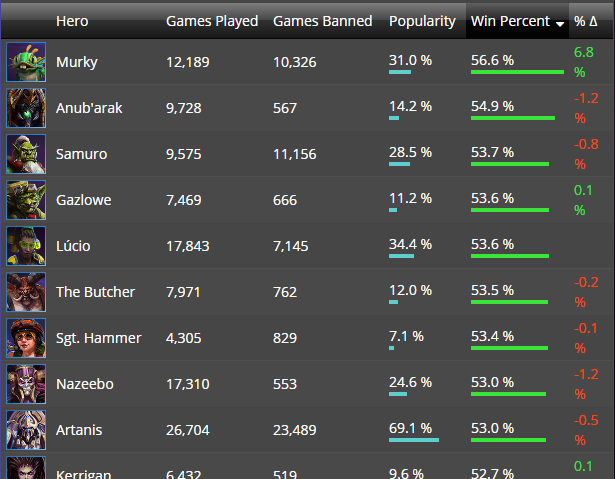
Look at all those juicy numbers from Hotslogs.com. So many numbers.
Now maybe you aren’t the sort of person that likes following the meta cookie cutter builds. Blazing your own path and discovering new interactions is a tremendously enjoyable activity. I know Adam is a mad genius in the realm of Netrunner Decks, and I’m pretty sure that Wyatt plays games exclusively to bamboozle his opponents with bizarre and off the wall strategies. Personally, I play to win because I am a sad, empty shell of a man. If data analytics can help me do that, then I’ll use a meta build if I can. Within the top tiers of play I can usually find a few strategies that tickle my fancy.
Making Your Own Luck
Really, my advice here isn’t really “Do what works for other people.” You need to do what works for you, so go ahead and bring that insane kitchen table build. Run it through the crucible. See what sloughs off. The metagame has it’s own section of math. Usually that boils down to “develop a toolkit that gives you what you need to get the game state to where you want it to be.” Usually before the game even starts you can stack the proverbial deck in your favor by bringing the most powerful cards, the most impactful talent choices, the most flexible skills. But once that happens, what do you do? In my attempts to understand the game in terms of numbers, I’ve developed some simple tricks to help gauge how to win on a per-game basis.

Give yourself the biggest advantage you can by avoiding dice like these.
I’ve been playing crunchy games since I was seven so I have had a fair bit of practice in the realm of analysis. I like to think I’m pretty good at it, too. There’s a couple of tips I can give you to help you determine what is the best way to win a game.
There’s some basic assumptions that I’m making here:
- You are playing a game that has some randomness.
- You are playing a game where you can predict that randomness with some degree of accuracy.
- You are playing a game that gives you control over the outcome in some way. That may be by expending resources, or just raw decision-making.
- These points deal with the game as it is being played, not pre-game where you are constructing your deck list for a tournament, or assembling your space marines for a tabletop war game.
So craps and roulette don’t work here, that’s just gambling. Chess doesn’t, not really, because that game is 100% skill. This is more for board games like Lords of Waterdeep or card games like Magic the Gathering. Now, I’m not going to claim to be excellent at Magic, but I’m hoping you can take these general concepts and play games with a more focused and actively cognizant approach to handling variance. Wyatt and my other gaming friends know my mantra: “What is the play here?” I ask myself that so I can make clear decisions about what I want to happen. It was a question that I learned to ask myself before I cast Brainstorm back when I was into the MTG Legacy format. I was giving myself lots of options, but before I could look at the cards I needed to figure out what I was actually hoping to see. What was my best case scenario? My worst? Only once I had an understanding of the possible outcomes could I make any kind of value judgement on what my options were.
Have A Goal And Stick To It
The simplest question you need to be able to answer is “How am I going to win?” If you don’t have a concrete plan then it’s impossible for you to judge what plays will be good and which will be bad. Figure out the destination, then hack a path through the proverbial jungle. You need to have an “ideal” board state, one that gives you the ironclad victory. Work for it.
What Is A Good Play?
In short, a good play is one that gives you the highest chance to win. ”Winning” in this context might not be the actual move of the game that awards the most victory points. Gathering the most resources in a turn, developing your capacity to win later, or even spending some time to maneuver yourself into a better position can be a win on a per-turn scale. If you accrue more of these small victories over your opponents, at the end of the game you’ll be sitting on a huge pile of points with the strongest board state. Many times you’ll be playing and realize that even though the game has another three or four turns before it ends, you’ve lost. That means that your opponents have managed to edge you out with a series of small victories. Oops. Git gud.
Given the option between making a play with a 70% chance of success and a play with only a 25% chance of success, the first play is the “good” play. Sometimes your best play may be one that gives you a 33% chance to win. There’s no point bitching about it, if that’s the best you’ve got then you should go for it.

4 monsters and a barrier vs 4 treasures. You know the odds.
What Is A Bad Play?
A bad play is quite simply any play that wasn’t the best one (see above for “good play”). As a related aside: I play games with my friend Kirsi who is an absolutely ferocious game player. She’s really f-ing good and beating her at basicly anything is nearly impossible. One time we were playing BattleCon, which has no hidden information and depends a lot on reading your opponent and knowing what they are going to do. I usually lose to Kirsi when we play it. In one turn, I knew what my best play was. However, I knew that she knew, so I guessed that her response would be her best play. I was able to figure out what the counter to her best play was. When I executed that counter play, I came out ahead. In this case, my best play wasn’t truly my strongest option, but rather the choice that invalidated Kirsi’s best play. Sometimes your best play will be hidden or be buried in a series of choices out of your control.
Proper Retroactive Analysis
Just because a good play didn’t work doesn’t make it a bad play. This is a fallacy that I see newer players, or those who are less acquainted with math, making. Sure a 90% chance is great, but one in every ten times it will fail. You can’t justify thinking “well if it didn’t work this time, then I shouldn’t do it again.” I used to do this a lot when I played Magic. The turn that I lost, I would check the top couple of cards of my deck and say “Oh, if I had only had this card one turn earlier, I would have won!”
No. That’s wrong.
You can’t justify your losses through bad luck. Granted, sometimes you’ll just catch the shaft and roll garbage all game. However, if the game has even a semblance of balance and good design, there is no individual match that you are entirely fated to lose from the start before either player has made any decisions. What you would have gotten if you had made different choices matters. What you would have gotten if your random shuffling had been different does not matter.

Making decisions harder since 1995!
When Can A Bad Play Be A Good Play?
Let's say that it’s the last turn of the game. Your opponent is ahead by 2 points. You are presented with two clear options on your turn: one play with a 80% chance to get you 1 point, and a play with a 10% chance to get you 3 points. Which is the better play?
If you’re going to lose anyway, there’s no point in going with the “safe” choice to get one point. You might as well throw out the hail mary in the hopes of actually walking away with the win. If the momentum of the game is going against you, sometimes you can’t play safe and maintain the status quo. When the status quo is against you, when it’s going to end up with you losing, you need to figure out how to shake it up. If you can be aware of when the flow of the game is against you then you can make more cognizant use of your tools to wrestle it back under your control.

I was playing the Star Wars: X-Wing Miniatures Game from Fantasy Flight Games the other day and my poor t65 was down to 1 hull point (basically dead). My opponent could very easily have blasted it out of the sky. Now, I had other ships in the air so it wasn’t a total loss but my t65 was in a very precarious position. I was presented with two options: Run, or fight. If I ran I could keep the t65 alive for some time, but I wouldn’t be able to leverage it as an asset in the ongoing fight. If my opponent didn’t chase it down, then I would basically have removed my own ship from the fight until I was able to bring it back into position three turns later. During that time my opponent could have brought the full force of their ships to bear against my now outnumbered little fleet. If I stayed and fought then I was 100% going to lose my t65 and be down a ship. Yet a fight between my damaged ship and my opponent’s damaged ship might result in me winning. I knew that if I ran, I was 100% going to be outnumbered and outmaneuvered. If I stayed, I had the chance, slim though it was, to take an enemy ship out of the air before I went down in flames. At the end of the round I was essentially going to be down a ship either way, so I took the play that had a chance to remove an enemy ship from play as well. I gambled my assets on the line of play that appeared worse: I was for sure going to lose a ship instead of keep it, but I was functionally giving my ship a last-ditch chance at evening the score. I’m not going to tell you how it turned out, because I think it was the best play I could have made at the moment.

Lots of options. Lots of lines of play.
Abandon Fruitless Strategies - Sunk Costs Fallacy
The sunk costs fallacy says that if you’re pursuing a path and you realize that it won’t work as well as another path, it’s better to continue on the “worse” option because you’ve already committed resources to it. Basically, you’re ascribing emotional weight to the cost you’ve laid out, even though it may objectively be not worth it in the end. If you can separate the emotional value from the real value of your resources you’ve put towards a plan, you’ll be better able to abandon a suboptimal play for a better one.
Let’s say you’ve spent some money on a railroad in Monopoly. First thing you should do is stop playing Monopoly and seriously examine your life choices. (Haha [I’m not kidding]). Your opponent has 2 of the other railroads. They offer a trade of your railroad for something else with a better return. Now maybe holding onto it to prevent your opponent from getting a better rent multiplier is a valid play. However, keeping it simply because you bought it and you haven’t gotten enough rent from the railroad to pay for it’s cost is fallacious. If you can leverage that property into something more valuable, like finishing a monopoly, then you’ve turned a sunken cost into an asset. If you keep your eyes open to turn wasted opportunities into new avenues of play you may just be able to spot lines of play that you would have missed otherwise. At worst, putting no further investment into a poor play is critical. Burning valuable resources on a play that will not reliably give a return is an easy and subtle way to lose a game.
Play Me Off, Sam
In conclusion, I think the key to playing games well often goes beyond the actual mechanics of the game itself. Quality play lies at the intersection of understanding a game’s mechanics and understanding a game’s theory. Knowing how to execute a certain play is important, but knowing WHY to execute that play, or maybe to wait, is also important. Mechanics can be learned from study, but theory can only be gleaned from playing the game (or reading good player’s treatises on theory).On a final note, here’s some basic math to keep in mind when playing games:The average result on a fair die is equal to the average of all its faces. For a d6 that is 3.5. A d20’s average is 10.5. The average 2d6 roll is 7, and the average 3d6 roll is 10.5. Rolling more small dice is better than rolling one big die because the probability distribution is a curve, not a line, and produces more reliable numbers.The average sum of the dice rolled in the header picture is approximately 92.5.An average draw from a 52 card poker deck is 7.An average tweet is not worth the time to read. Check us out at @SpritesNDice. Check out our Patreon. Check out our streams and podcasts. They are decidedly above average.